 A
A
In the year 1867, Hermann von Helmholtz had suggested a method to measure the distortion of the human eye (more precisely: the distortion of the human visual field). It works as following:
A particularly prepared checkerboard is watched from a well defined distance. This checkerboard has got a certain amount of pincushion distortion. Amazingly, when watched close up, it suddenly appears regular! This is the result of a residual distortion inside the human visual field.
However, it is not generally known how strong this distortion would be, or, more precisely, there appears to be quite a bit of scattering between different individuals, and the statistical distribution of this distortion among the population is still under investigation. Hence, I have asked volunteers on the Internet to do the test and report their results.
This is how it was done: Below are 6 checkerboards with an increasing amount of pincushion distortion. It is possible to click onto the thumbnails to load the larger versions of the images. At the bottom of each checkerboard there is a black bar. The length of this bar indicates the distance from which the board should be observed. During observation, it is important to strictly fixate the center of the board , with a single eye, and simultaneously judge whether or not the checkerboard looks straight. The volunteer was requested to not let his direction of view drift away from the center, because in this case the contours appear to bend and it becomes impossible to measure the distortion of the visual field accurately.
 A
A
A total number of 56 people have participated in the experiment. Thanks a lot for your efforts, may these data lead to a new generation of improved binoculars! This is the distribution of votes for the different checkerboards:
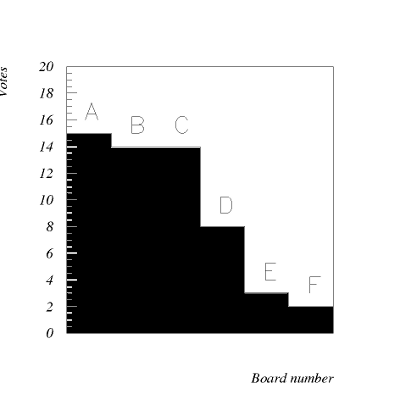
It is obvious that the first three boards have received about the same number of votes. Beyond that, the scores are dropping. The overwhelming number of participants declared to wear glasses, hence I did not separate the results into spectacle- and non-spectacle wearer, since the latter would not have delivered sufficient statistics.
The checkerboards shown above were generated using the following generalized imaging equation (see this web-page for a detailed explanation):
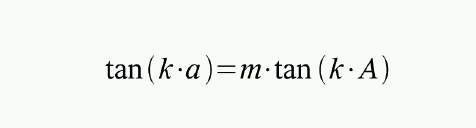
For these examples I assumed a 10x wide-angle binocular with 7 degs. true field of view. The amount of pincushion distortion was successively increased from k=1 (checkerboard A, no distortion) to k=0 (board F, angle condition). The exact values are:
If we simply take the mean value of the above results, then we obtain an average value for the distortion of the test persons' visual space near k = 0.76, which is in close agreement with the results presented by A.H.J. Oomes et al., Perception 38, p. 1284, 2009, who have carried out a similar experiment in their laboratory. However, in order to interpret these numbers correctly, one has to take into account potential sources of systematic errors:
During the experiment, the test person was requested to exactly fixate the center of each checkerboard, and to judge the curvatures of the contour lines through monocular observation. However, such a fixation was not enforced, neither by the present setup nor by the experiments of Oomes et al. It may well be that in particular inexperienced observers may not have kept their direction of view exactly put at the center, but, consciously or unconsciously, may have moved the eye around a little bit. In such a case they would have observed the curved lines of the pincushion-distorted contours, and would possibly have chosen another checkerboard, one with less distortion, as the one they perceived uncurved. This type of error cannot be corrected for by the setup of this experiment, and it always generates a bias toward lower distortion, never toward higher distortion.
Hence, the resulting average distortion of k = 0.76 may serve as a lower limit only (in terms of distortion, the k-value would be an upper limit), the actual average being most likely shifted to higher distortion (i.e. lower values of k). Oomes et al have also reported that rather experienced observers seemed to have chosen checkerboards with higher distortion, while casual observers did, to a higher percentage, choose those with lower distortion, perhaps because some of them did not carry out the experiment with the necessary amount of precision.
I would assume that the true average k-value would be close to k=0.7, perhaps even a little lower. Helmholtz had suggested a value of k=0.5, which would be checkerboard E, but it seems that this can quite safely be ruled out, even after considering a possible systematic shift.
Which consequences are to be drawn for the binocular manufacturer? With a choice of pincushion distortion near k=0.7, the majority of users would not complain about any globe effect. To be on the safe side, one might want to go a little lower, perhaps between k=0.6 and k=0.7, accepting a little bit of an extra pincushion distortion. In any case, the extremes should be avoided, namely values of k<0.5 (too much pincushion) or k>0.8 (too much of a globe effect). Additionally, the distortion curves should be smooth, avoiding any local extrema or inflection points. As a negative example, one might take a look at the BPO 7x30 with a strongly anomalous distortion curve. Keep it smooth, use the above imaging equation as a guidance, this would avoid any spurious curvature effects during panning.
Last updated: Nov. 2012